阻力部分
总论
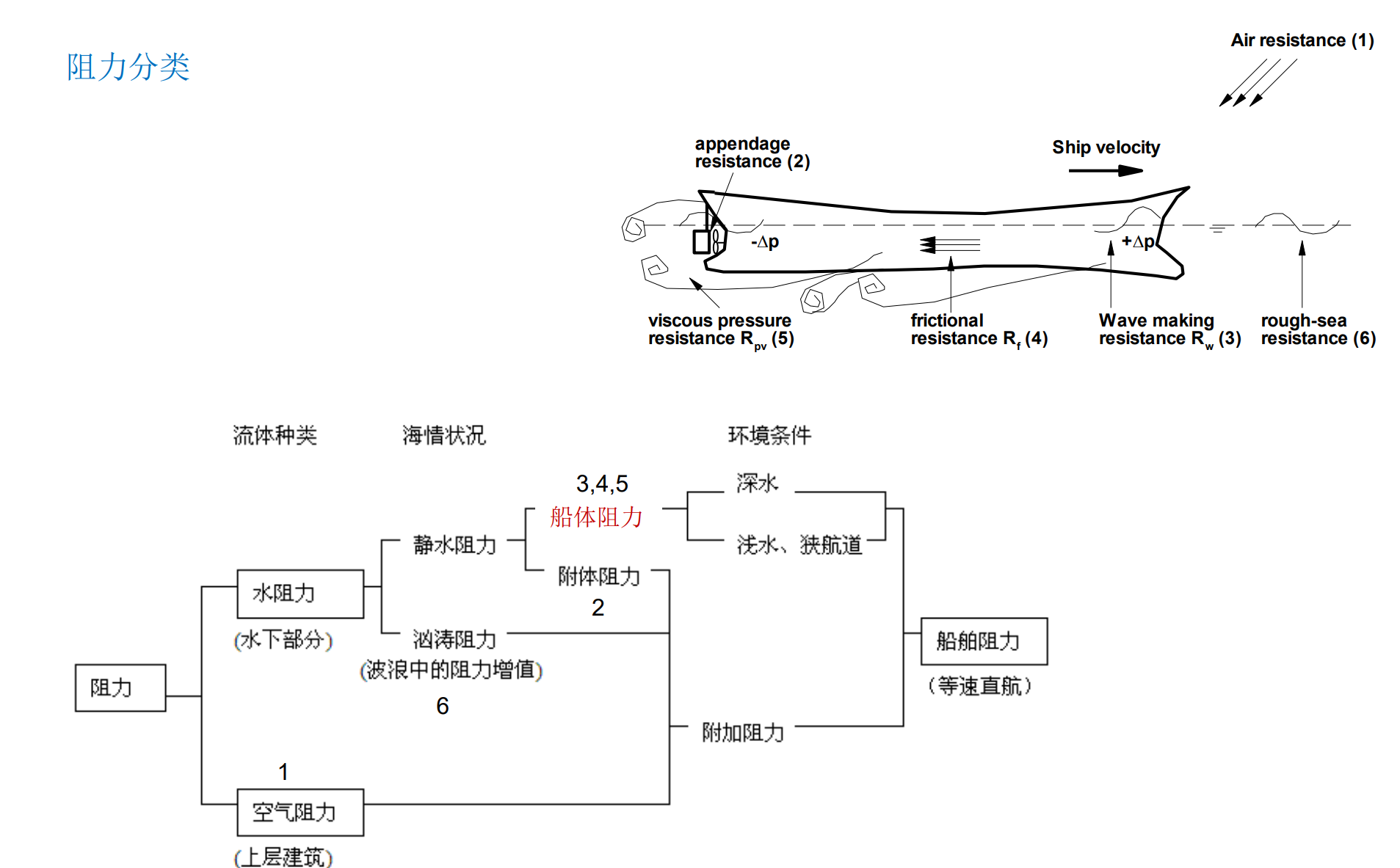
船舶阻力的成因及分类
阻力成因
空气阻力
附体阻力(舵、舭龙骨、轴支架等)
兴波阻力(波浪改变船体表面压力分布)
摩擦阻力(船体表面水粘性切应力的合力)
粘压阻力(流体粘性引起漩涡)
汹涛阻力(波浪增阻)
船体阻力计算及分类
研究范围:等速直航
船体阻力$R_t$=兴波阻力$R_w$+摩擦阻力$R_f$+粘压阻力$R_{pv}$
摩擦阻力和粘压阻力合称粘性阻力,粘压阻力和兴波阻力合称压差阻力
注:压阻力中包含有粘压阻力和兴波阻力两类不同性质的力。兴波阻力既使在理想流体中仍然存在,而摩擦阻力和粘压阻力两者都是由于水的粘性而产生的(可合称为粘性阻力),在理想流体中并不存在
阻力成分的比例
低速船:摩擦阻力70%~80%,粘压阻力10%以上, 兴波阻力很小
高速船:兴波阻力40%~50%,摩擦阻力50%,粘压阻力5%
阻力曲线
船型给定时,阻力仅仅是船速的函数。
有效功率(克服船体阻力所需功率):$P_E=船体总阻力R_t\times船速 v_s$
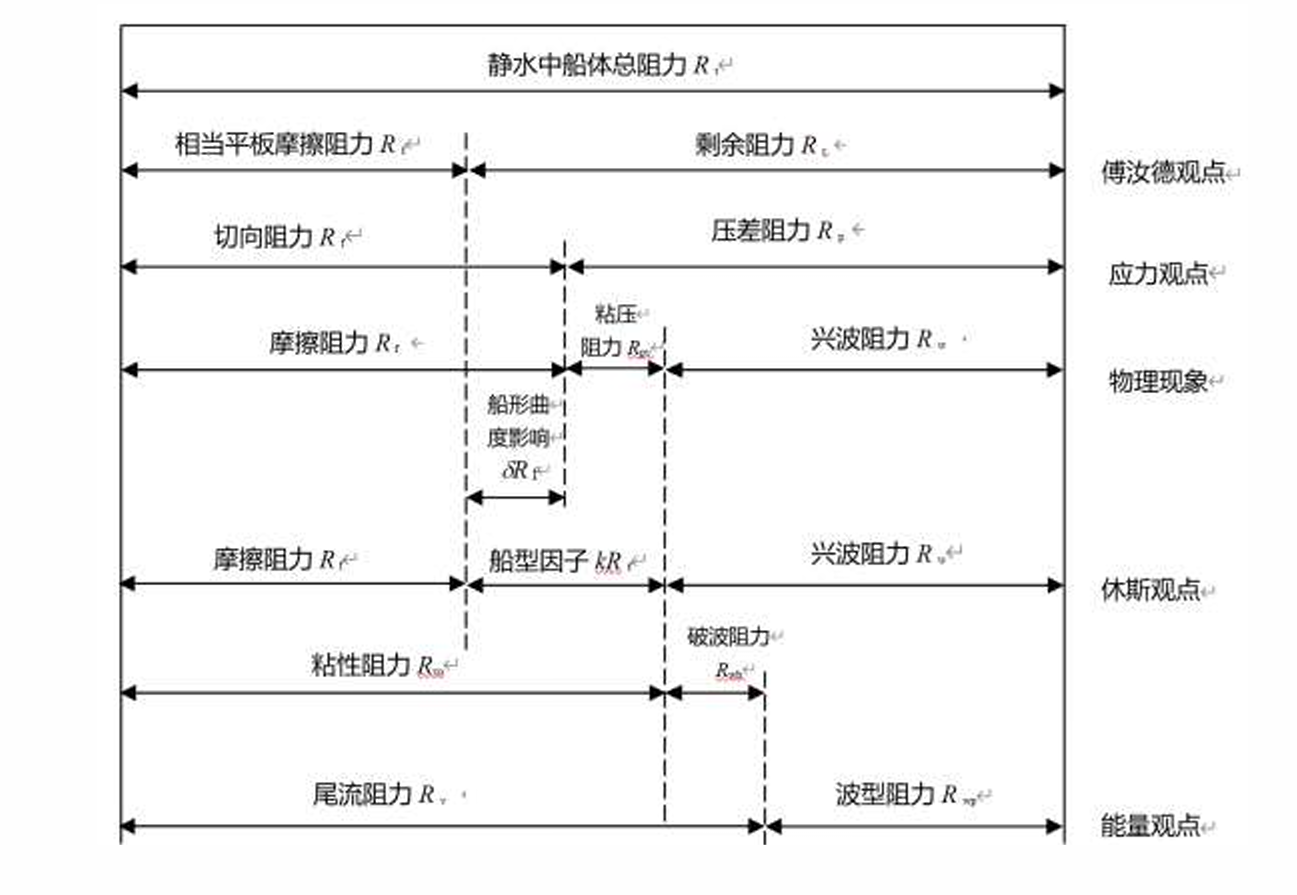
傅汝德阻力分类
船体阻力$R_t$ = 摩擦阻力$R_{fp}$ + 剩余阻力$R_r$
此处$R_{fp}$为相当平板(船长与湿表面积相等的平板)的摩擦阻力
阻力相似定律
相似理论和量纲分析
力学相似=几何相似+运动相似+动力相似
量纲分析中的$\pi$定理
粘性阻力相似定律——雷诺定律
一定形状的物体,粘性阻力系数仅与$Re$数相关;
当$Re$数相同时,两形似物体的粘性阻力系数相等。
粘性阻力系数$C_v=f(Re)$
$$C_v=\frac{R_v}{\frac{1}{2}ρV^2S}$$
$$Re=\frac{VL}{\nu}=\frac{\rho VL}{\mu}$$
ρ、μ为流体密度和动力粘性系数,𝜈为运动粘性系数,V、L为 流场的特征速度和特征长度。
在典型的海洋工程应用中,比如船舶、海洋平台中:$Re=10^{6-10}$
因此粘性影响一般可忽略;但对粘性阻力问题不可忽略。
兴波阻力相似定律——傅汝德定律
考虑在理想流体中航行的水面船舶,由于流体无粘,所以既无摩擦阻力又无粘压阻力,仅有兴波阻力。
$$C_w=f(Fr)$$
$$C_w=\frac{R_w}{\frac{1}{2}ρV^2S}$$
$$Fr=\frac{V}{\sqrt{gL}}$$
形似船之间,为保持$Fr$相同,则它们速度必须满足一定的关系:
$$V_m=\frac{V_s}{\sqrt{L_s/L_m}}$$
- 当模拟具有自由液面的液体流动时,如水面船舶运动、明渠流动等,$Fr$数是必须考虑的相似准则数
- $Fr$数较小表示绝大部分船重由浮力平衡,即船舶处于排水航行状态;$Fr$较大表示绝大部分船重由水动升力平衡,使它处于全滑行状态。
船体总阻力相似定律——全相似定律
$C_t=f(Fr,Re)$
全相似做不到。船模与实船之间的运动差异是由于模型与实物之间相似条件不能全部满足而给换算带来误差,称为“尺度效应(Scale Effect)”
二因次法求船体阻力
Froude假定——二因次法:船体总阻力$R_t$分为两个部分:
摩擦阻力$R_f$只与$Re$数有关,船体的摩擦阻力等于同速度、同长度、同湿面积的平板摩擦阻力(相当平板假定 )
剩余阻力$R_r$ = $R_w$(兴波) + $R_{pv}$ (粘压) 只与 $ F_r$ 数有关并满足比较律
阻力形式:$R_{ts}=R_{fs}+(R_{tm}-R_{ts})\frac{ρ_s}{ρ_m}α^3$
无量纲阻力系数形式:$C_{ts}=C_{fs}+C_{rs}+\Delta C_f$
$C_{fs}$可从湍流平板公式求得,$C_{rs}$可由相似定律求得$𝐶_{𝑟𝑠} = 𝐶_{𝑟𝑚} = 𝐶_{𝑡𝑚}(实验测定)− 𝐶_{𝑓m}(平板公式)$,$\Delta C_f$为船体粗糙度修正
阻力形式Froude法换算的一般步骤:
- 船模实验测得船模的船体阻力$R_{tm}$
- 以相当平板假定为基础,计算出船模的摩擦阻力$R_{fm}$
- 求船模的剩余阻力$R_{rm}$
- 应用比较定律换算出实船的剩余阻力$R_{rs}$
- 以相当平板假定为基础,计算出实船的摩擦阻力$R_{fs}$
- 求实船的船体阻力$R_{ts}$
静水阻力与船桨相互作用
摩擦阻力
粘性阻力的组成与船体边界层
粘性阻力的组成:
摩擦阻力:水的粘性作用,船体表面产生摩擦切应力
粘压阻力:水的粘性作用,船体前后部分存在压力差
船舶粘性阻力的计算方法:
根据边界层理论或雷诺平均方程用数值方法求解
工程上,将摩擦阻力和粘压阻力分别求解
船体边界层
船体边界层的特点:
- 船体几何形状十分复杂,数学表达困难。
- 边界层外缘势流与平板的势流明显不同。平板:边界层外缘势流速度和压力均保持不变;船体:势流是三维的,存在纵向的速度梯度、 压力梯度,首尾尤显著。
- 船前75—80% L是薄边界层,以后边界层变厚。 压力在边界层内有变化,要用N-S方程解。
平板边界层与摩擦阻力
层内的流动状态取决于局部雷诺数
层流:$Re<(3.5-5.0)\times 10^5$
转捩:$(3.5-5.0)\times 10^5<Re<3.0\times 10^6$
湍流:$Re<3.0\times 10^6$
平板受到的摩擦阻力:
$$C_f=\frac{R_f}{\frac{1}{2}\rho v^2S}=\frac{1}{x}\int_0^x{C_{\tau}dx}$$
对于层流边界层有Blasius解:
$C_\tau=0.664Re^{-\frac{1}{2}}$
$C_f=1.328Re^{-\frac{1}{2}}$
对于湍流平板边界层:参见《水动力学基础》刘应中等
另一种近似(幂次率):$\frac{u}{\nu}=\left( \frac{y}{\delta} \right) ^n, n=\frac{1}{7}\sim \frac{1}{11}$,n的具体取值与雷诺数有关。
Karman动量方程:略
平板摩擦阻力系数计算公式
湍流平板摩擦阻力公式:
- 由幂次律(指数律)得到的平板公式
- 由对数分布得到的平板公式
- Schoenherr(桑海)公式
- Prandtl-Schlichting(柏兰特-许立汀)公式
- Hughes(休斯)公式
- ITTC公式:$C_f=\frac{0.075}{(\lg Re-2.0)^2}$
层流段、过渡区的影响:略
船体表面弯曲度对摩擦阻力的影响
船体水流均速>平板,在船前70%部分边界层厚度小,摩擦阻力偏大;
当船尾附近,船体边界层增厚,水流速度减小,摩擦阻力随之减小。
总体来说船体表面弯曲度对摩擦阻力影响并不显著。这也表明想通过改变船体曲线的办法来减小摩擦阻力,其效果不明显。
对于三维的回转体来说,弯曲度对摩擦阻力的增加并不明显。但对二维物体的影响大得多。
注意:这只是曲率对C𝑓的影响,粘压不在内(不考虑漩涡影响)
船体形状效应:船体形状引起的船体摩擦阻力与相当平板摩擦阻力差别
形状因子 $k_f$:
实际船参照$k_f$与L/B的关系图, $𝑘_𝑓$在1.00—1.03之间较小,故一般认为,船体弯曲度对摩擦阻力的影响并不显著。
船体表面粗糙度对摩擦阻力的影响
船体表面粗糙度:普遍糙度、局部糙度(结构糙度)、污底。
实践证明,船体表面粗糙度对摩擦阻力的影响是很显著的。
$Re$较小时,粗糙度不起影响,接近光滑曲线;
$Re$较大时,粗糙度产生影响,阻力曲线逐渐离开光滑曲线:$C_f=f(Re,L/k_\sigma)$
$Re$很大时,$\Delta C_f$与雷诺数选取无关,为常数
摩擦阻力计算
$Re>10^7$, $\Delta C_f=0.4\times 10^{-3}$为常数
1975年ITTC公式:$\Delta C_f=\left[ 105\left( \frac{k_s}{L} \right) ^{-\frac{1}{3}}-0.64 \right] \times 10^{-3}$
基本步骤:
- 计算雷诺数:$Re=\frac{vL}{\nu}$
- 计算光滑平板的摩擦阻力系数:Schoenherr公式 ,Prandtl-Schlichting公式, 15th ITTC公式
- 使用S或P-S公式,则$C_a=\Delta C_f=0.4\times 10^{-3}$
1975年ITTC公式 $L_w<150m$
1990年ITTC公式 $L_w>150m$ - 计算船舶湿表面积$S$
- $R_f=\frac{1}{2}(C_f+C_a)\rho v^2S$
减小摩擦阻力的方法
传统思路:使湿表面积减少;使表面尽可能光滑;减少不必要的附体
其他思路:将船体抬出水面,减小ρ;气膜减阻;控制边界层;高分子减阻(在船体表面不断喷注高分子添加剂);软性(顺应)覆盖层(如海豚表皮);表面波纹和沟槽
粘压阻力
船体粘压阻力产生原因
边界层的动量损失,在船尾部形成漩涡
影响粘压阻力的因素
- 最重要的是物体后端的形状——减小纵向的逆压梯度
- 边界层的流动状态;船模和实船$Re$相差$10^3$左右,边界层分离不相似,往往船模分离而实船 不分离
- 船体的舭涡——安装球鼻首
降低粘压阻力对船型的要求
- 注意后体形状
- 船型变化不宜过急,特别注意横剖面曲线A(x),前肩勿过于隆起,后肩勿过于内凹
- 对低速肥大船型,可采用球鼻艏以减少舭涡
- 注意方形系数的选取
- 肥大船型:$C_B>0.8,\frac{L}{B}>6$ 分离不可避免
船体粘压阻力处理方法
Froude法(二因次法):随船长的增大,更主要的是肥大船的出现,Froude 法不适用
1+k方法(三因次换算法):
- 减小Cr中不符合比较定律的部分,提高$C_{fp}$在船模端的数值
- 将粘压阻力以形状因子并入摩擦阻力
$$C_t=(1+k)C_{fp}+C_w$$
$$C_{ts}=C_{tm}-(1+k)(C_{fpm}-C_{fps})+\Delta C_f$$
k——形状系数:
形状因子$$(1+k)=\frac{C_v}{C_{fp}}$$
k的确定:1978年ITTC改进Prohaska法:假定$C_w\propto F_{n}^{m}, m=4到6$,(Prohaska法取m=4)
$$\frac{C_{tm}}{C_{fpm}}=(1+k)+y\frac{F_{n}^{m}}{C_{fpm}}$$
(1+k), y, m根据船试验结果用最小二乘法来确定
确定粘性阻力的尾流测量法
利用动量损失来间接测量粘性阻力
兴波阻力
船行波的形成和Kelvin波系
两类兴波:
船行波:留在船后方并不断向外传播的波浪
破波:并不以波浪的形式留在船后,主要发生在肥大船型
兴波阻力:
- 由船行波产生的阻力称为波形阻力,是船舶兴波阻力的主要成分
- 由破波产生的阻力称为破波阻力,在船舶兴波阻力中所占比重较小
- 若无特殊说明,通常船舶兴波阻力是指波形阻力,而不包括破波阻力
平面进行波的特征:
- 波长:$\lambda$
- 波数:$k=\frac{2\pi}{\lambda}$
- 周期:$T$
- 圆频率:$\omega=\frac{2\pi}{T}$
- 波速:$c=\frac{\omega}{k}=\frac{\frac{2\pi}{T}}{\frac{2\pi}{\lambda}}=\frac{\lambda}{T}$
- 深水色散关系:$\omega^2=gk$
- 周期T,波速c、波长$\lambda$的相互关系
波能:
波浪运动所具有的能量,包括波浪的动能和位能
在单位自由表面上,平面进行波的时间平均总能量:
$$E_0=E_k+E_p=\frac{1}{4}\rho gA^2+\frac{1}{4}\rho gA^2=\frac{1}{2}\rho gA^2=\frac{1}{8}\rho gH^2$$
波能传播速度(群速度):
由于位能和动能各占总能量之半,且动能不沿波形传播方向转移
因此就波浪总能量而言,其传播速度仅为波速之半:$C_E=\frac{1}{2}C$(深水)
船行自由波:
船行波的形成:
- 船舶航行时,改变船舶四周的流场及压力分布,而形成波。
- 实际船行波的首波峰总在船首柱稍后的地方;尾波峰位于尾柱之后,尾柱前总为一波谷。
船的首尾波系及其干扰
船行波的主要特征:
首尾两大波系:首横波,首散波;尾横波,尾散波
整个波系限定在凯尔文角所限定的范围内
首横波在艏柱略后处为波峰;尾横波在尾柱略前处由波谷开始
整个波系,横波之间及散波之间互不干扰
船首尾两横波在船尾互相混合,组成合成横波
船行波随船一起前进,因此波速等于船速:$c=v_s=\sqrt{\frac{g\lambda}{2\pi}}$
首尾肩波:船型突变 导致压力突变而形成
首尾横波的干扰:有利(峰+谷)和不利干扰(峰+峰,谷+谷)
影响首尾横波干扰的因素:
兴波长度mL:首横波第一波峰与尾波第一波峰之间的距离
干扰结果取决于兴波长度mL和波长$\lambda$:
$$mL=n\lambda+q\lambda$$
$$n+q=\frac{m}{2\pi Fr^2}$$
式中,n为正整数;q为正分数;m为系数,主要与傅汝德数和船型有关
q=0,首尾横波重合,不利干扰
q=0.5,首尾波波峰波谷重叠,有利干扰
q为任意分数,一般干扰
兴波阻力和波浪参数
$$R_w=\frac{1}{4}\rho ga^2$$
兴波阻力与波高的平方成正比。当波高增加时,兴波阻力急剧增加。
兴波阻力的一般规律
$$R_w=[A+Bcos(2\pi \frac{mL}{\lambda})]v^6$$
$$C_w=\frac{R_w}{\frac{1}{2}\rho v^2S}=(C+Dcos(2\pi \frac{mL}{\lambda}))(\frac{v}{\sqrt{gL}})^4$$
不同船型的兴波阻力差异
- 当Fr<0.15,兴波阻力较小
- 在整个Fr区,丰满船的Cw比瘦削型的高速船大,在Fr增大时,两者的差极为明显。
- 丰满船在低Fr数时,Cw出现峰谷;瘦削型仅在Fr=0.5附近存在峰值。
- 随航速变化很大 $R_w~v^6$, $C_w~Fr^4$
- 随船型变化很敏感(对比摩擦阻力$R_f$,与湿面积成正比)
- 兴波阻力曲线有起伏 (波阻峰点,波阻谷点)
设计时力求避免在峰点,办法:
①改船长
②改船速 ,影响波长
③调整菱形系数Cp, Cp对阻力有一定影响
兴波阻力与船型关系及干扰预测
圆圈P理论预测兴波干扰:
设首横波第一个节点到尾横波第一个波谷之间的距离为CpL(棱形系数乘以船长),则:
$$mL=CpL+\frac{3}{4}\lambda$$
$$\frac{CpL}{\lambda}=(n+q)-\frac{3}{4}$$
当q=0.5时有利干扰:$C_pL/\lambda=n-1/4$
当q=0时不利干扰:$C_pL/\lambda=n-3/4$
定义圆圈P$=\frac{v}{\sqrt{\frac{gC_P L}{2\pi}}}=\sqrt{\frac{\lambda}{C_p L}}$
圆圈P为船速与波长为$C_p L$时的波速的比值
可以根据圆圈P预测兴波阻力的峰谷
波阻峰:圆圈P=$\sqrt{1/(n-\frac{3}{4})}=\sqrt{4},\sqrt{4/5},\sqrt{4/9},\sqrt{4/13}……$
波阻谷:圆圈P=$\sqrt{1/(n-\frac{1}{4})}=\sqrt{4/3},\sqrt{4/7},\sqrt{4/11},\sqrt{4/15}……$
实际应用:$P=2.5066\frac{Fr}{\sqrt{C_p}}$,制作预测图谱
确定兴波阻力的方法
船模试验法
Michell的“薄船”兴波阻力 Rw的计算公式,影响兴波阻力主要是水线的纵向梯度
波形分析法
减小兴波阻力的方法
减小常规船兴波阻力的方法
常规船,尤其是中速船,0.2<Fr<0.3,经典方法:
恰当选择主尺度和船型系数L/B, Cp, 首部进流段,进水角等
以实验资料,圆圈P理论为依据,当船速给定时,避免处于波阻峰点
船型优化,主要依据Michell理论,应用现有优化技术,选择f(x,z)使Rw最小。有时船型改变不大,但能收到明显效果
造成有利干扰:球鼻首。船首兴波与球鼻首兴波产生有利干扰,可使总阻力下降10-15%.
军舰、高速船由于首波峰的位置随航速后移,装球鼻首后无用,有装消波水翼的
应用不同设计概念减小兴波阻力:双体船和多体船概念;使船体抬出水面设计概念;船体下潜设计概念;复合设计概念
破波阻力
成因:
对于方形系数较大的肥大船型,艏部水线进角大,艏柱又很陡直,对来流产生严重的阻塞作用,导致波峰翻卷,波浪破碎, 在破碎的波面周围和其后面形成湍流,在湍流的形成过程中伴随着有序运动的能量耗散, 这股湍流在扩散的过程中随来流流向船后尾流,由于有序运动的损失,显示出动量的亏损, 这种能量的损失或动量的亏损,体现为破波阻力。
特征 :
⚫ 波浪在首柱面向外翻卷
⚫ 卷入空气,出现白色泡
⚫ 破碎后以湍流形式流向后方,留在尾流中,而不再以波浪能量出现,故可在尾流中测量
特性:
⚫ 是由于自由面引起的。将重叠模进行深水拖曳并进行尾流测量, 没有发现次尾流区
⚫ 破波阻力随Fn增大而增大,而且服从Froude的比较定律,即Fn数相等时,破波阻力系数相等
⚫ 丰满船破波阻力较大,压载情况下破波阻力要比满载时大,因为压载时B/T值增大
⚫ 破波阻力除了与船型有关外,主要与B/T和进流段长度有关。减少 B/T,增大进流段长度,将能明显减少破波阻力
⚫ 理论和实验都证明,采用球鼻型船首能减少破波阻力,主要原因是减少船首波的陡直程度,而且球鼻型的船首在轻载(压载)时效果较大
阻力分类补充说明
附加阻力及总阻力近似估算
附体阻力
实船需安装舵、舭龙骨、轴包架、轴和轴支架、声纳等附体(不含螺旋桨),由于水对附体作用而增加的那一部分阻力称为附体阻力。
由于附体通常安装在水线以下较深的位置,且相对尺寸较小,兴波阻力通常很小,因而认为附体阻力的主要成分是摩擦阻力和粘压阻力。
支架等较短的附体,主要是粘压阻力,并可认为其阻力系数与速度无关;而舭龙骨、轴包套等较长的沿流线方向安装的附体,主要是摩擦阻力。
确定附体阻力的方法:
- 应用已有资料或经验公式估算
- 应用模型试验确定附体阻力:通过带附体和不带附体船模试验所得到的总阻力之差来确定附体阻力;尺度效应;附体系数
空气阻力
船舶在航行中、船体水线以上部分和上层建筑与空气的相互作用而受到的阻力。
在空气阻力中,摩擦阻力只占极小部分,而主要部分是粘压阻力。它与船舶水上部分的外形以及与风的相对速度大小和方向有关。
波浪中的阻力增值
汹涛阻力:船在风浪中航行时所增加的阻力称为波浪中阻力增值或称为汹涛阻力,记作Raw。
其大小与风浪大小、方向及船型、航速等因素有关。
引起波浪阻力增加的原因:
- 船体运动(主要是纵摇、升沉运动的影响)。与船体运动的幅值等参数有关
- 船体对波浪的绕射作用:波浪遇到船体后,被船体绕射而产生反射波,该水波的能量就是船体阻力增值的一部分。
波浪中的阻力增值问题相当复杂,已有的研究表明,影响波浪中阻力增值的因素主要有波浪和船型两方面。
波浪阻力增值的处理与储备功率:
- 由于波浪阻力增加,在保持静水中相同功率时,航速必然下降,这种航速的减少称为速度损失或简称失速。
- 考虑波浪阻力增值,如要维持静水中相同航速,则功率必须较静水功率有所增加,所增加的功率称为储备功率。
总阻力近似估计
- 根据船模系列试验资料估算阻力
- 根据经验公式估算
- 根据母型船数据估算
海军系数法:船型相近,大小速度差不多,主机类型相同,载重量、海况大致一样:海军系数C相同,C越大表示快速性越好
$$C=\frac{\Delta^{\frac{2}{3}}·V^3}{P_e}$$
船模阻力试验
略
船型对阻力的影响
基本概念
优良船型的含义:
阻力性能优良船型是对某一定速度范围和航行环境而言的;讨论船型对阻力的影响必须与设计船速度范围相联系(未来将同时考虑航行环境)
船舶分类及其主要阻力成分:
低速船:Fr< 0.20
Rw很小, Rf与Rpv 主要;所以要减小Rf和Rpv,
Rf ∝S —减小S —船型肥短 —易产生旋涡—去流段防止Rpv增大
中速船 0.20<Fr < 0.30
Rw随V提高而增大, 既要减小Rw又要防止Rf和Rpv↑,
办法:选择有利船型参数 —(兴波)有利干扰
船型趋于瘦削—避免旋涡,减小粘压阻力
高速船 Fr>0.30
Rw成为主要成分,力求减小Rw
办法:减小船首波系的波高—船体(前体)瘦长
高速船波浪长度大—首波在船尾难以实现有利干扰
船体主尺度的影响
排水量长度系数(瘦长系数)$\frac{\Delta}{(0.01L)^3}$
由L变化,$\frac{\Delta}{(0.01L)^3}$的影响:
低速船:摩擦阻力占总阻力的主要成分,可达总阻力的70%以上。而Rr所占比例较小,因此当排水量一定时,尽可能L 减小,船型肥短,对阻力-舱容-造价均有利
高速船:剩余阻力占总阻力的比例较大,因此随着船长增大,即$\frac{\Delta}{(0.01L)^3}$减小,总阻力的变化情况与低速船有所不同,存在最佳船长Lopt